PCFG Generator

Generate tree and sequences from a PCFG in Chomsky normal form.

import numpy as np
from triangularmap import ArrayTMap

PCFG generator:

class PCFG:

    def __init__(self, start, rules):
        self.start = start
        self.rules = rules

    def transition(self, symbol, *args, **kwargs):
        try:
            rules = self.rules[symbol]
        except KeyError:
            raise RuntimeError(f"Missing rule for {symbol}")
        right_hand_sides = np.empty(len(rules), dtype=object)
        right_hand_sides[:] = [r[0] for r in rules]
        weights = np.asarray(
            [r[1](*args, **kwargs) if callable(r[1]) else r[1] for r in rules],
            dtype=float
        )
        probs = weights / weights.sum()
        rhs_symbols = np.random.choice(right_hand_sides, size=1, p=probs)[0]
        return rhs_symbols

    def generate_tree(self, max_depth=None, verbose=0):
        # tree represented by its root
        root = {'symbol': self.start, 'children': []}

        # generate tree
        def recurse(front, depth=0, max_depth=max_depth):
            if depth > max_depth:
                raise RuntimeError(f"Current depth of {depth} exceeds maximum depth ({max_depth})")
            new_front = []
            for node in front:
                rhs_symbols = self.transition(node['symbol'], depth)
                for s in rhs_symbols:
                    child = {'symbol': s, 'children': []}
                    if len(rhs_symbols) > 1:
                        new_front.append(child)
                    node['children'].append(child)
            if new_front:
                recurse(front=new_front, depth=depth + 1)
        recurse(front=[root])

        # get the start/end indices and terminal sequence
        def process(node, start=0):
            terminals = []
            if node['children']:
                s = 0
                for c in node['children']:
                    s_, t_ = process(node=c, start=start + s)
                    s += s_
                    terminals += t_
            else:
                s = 1
                terminals.append(node['symbol'])
            node['start'] = start
            node['end'] = start + s
            return s, terminals
        n, terminals = process(root)

        # return root
        return root, n, terminals

    @classmethod
    def get_tmaps(cls, root, n):
        binary_tmap = ArrayTMap(n, 0)
        symbol_tmap = ArrayTMap(n, "", dtype=object)

        def fill(node):
            binary_tmap[node['start'], node['end']] = 1
            symbol_tmap[node['start'], node['end']] = node['symbol']
            if len(node['children']) > 1:
                for n in node['children']:
                    fill(n)
        fill(root)

        return binary_tmap, symbol_tmap

Define musical grammar and generate sequence.

Control sequence length with dynamic terminal weight, which becomes high non-zero from a certain depth on.

Rules is a dictionary the form {“left-hand-symbol”: [([“right-hand-symbols”, …], weight), …], …}

split_weight = 1
terminal_weight = lambda depth: 1e10 * int(depth > 2)

pcfg = PCFG(
    start="I",
    rules={
        "I": [(["I", "I"], split_weight),
              (["V", "I"], split_weight),
              (["C"], terminal_weight)],
        "IV": [(["I", "IV"], split_weight),
               (["F"], terminal_weight)],
        "vii0": [(["IV", "vii0"], split_weight),
                 (["B0"], terminal_weight)],
        "iii": [(["vii0", "iii"], split_weight),
                (["Em"], terminal_weight)],
        "vi": [(["iii", "vi"], split_weight),
               (["Am"], terminal_weight)],
        "ii": [(["vi", "ii"], split_weight),
               (["Dm"], terminal_weight)],
        "V": [(["ii", "V"], split_weight),
              (["G"], terminal_weight)],
    }
)

Generate a tree and sequence and get representation in TMaps, ready for plotting etc

root, n, terminals = pcfg.generate_tree(max_depth=100, verbose=1)
binary_tmap, symbol_tmap = pcfg.get_tmaps(root, n)

print(binary_tmap.pretty(crosses=True))
print(symbol_tmap.pretty(crosses=True))
print("   ".join(terminals))

        ╳
       ╳1╳
      ╳0╳0╳
     ╳0╳0╳0╳
    ╳0╳0╳0╳0╳
   ╳1╳0╳0╳0╳1╳
  ╳0╳0╳0╳0╳0╳0╳
 ╳1╳0╳1╳0╳1╳0╳1╳
╳1╳1╳1╳1╳1╳1╳1╳1╳
                ╳
               ╱ ╲
              ╳  I╳
             ╱ ╲ ╱ ╲
            ╳   ╳   ╳
           ╱ ╲ ╱ ╲ ╱ ╲
          ╳   ╳   ╳   ╳
         ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲
        ╳   ╳   ╳   ╳   ╳
       ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲
      ╳  V╳   ╳   ╳   ╳  I╳
     ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲
    ╳   ╳   ╳   ╳   ╳   ╳   ╳
   ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲
  ╳ ii╳   ╳  V╳   ╳  I╳   ╳  I╳
 ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲ ╱ ╲
╳ vi╳ ii╳ ii╳  V╳  V╳  I╳  I╳  I╳
Am   Dm   Dm   G   G   C   C   C

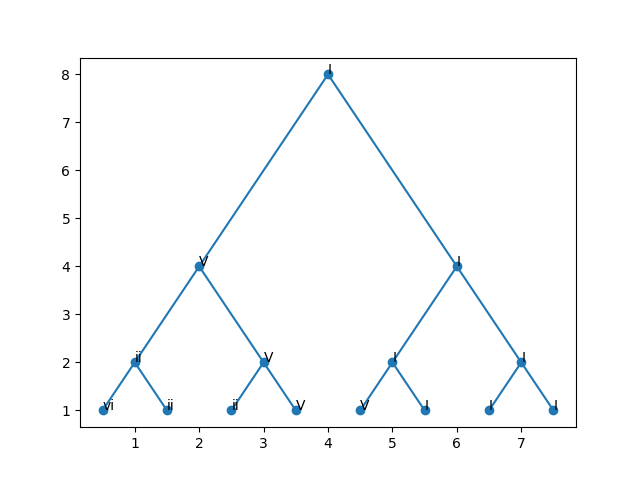
Import plot_tree function from other example and plot tree and labels:

from examples.plot_tree_from_tmap import plot_tree
import matplotlib.pyplot as plt

plot_tree(binary_tmap, label_tmap=symbol_tmap)
plt.show()