Note
Go to the end to download the full example code.
Optimising the Rosenbrock function
This runs stochastic gradient descent, specifically Adam, on the Rosenbrock function.
Define an Objective function module with loc and optimum that is later used for plotting.
from abc import ABC, abstractmethod
import torch
from torch.nn import Module, Parameter
from torch.optim import Adam
from torch.optim.lr_scheduler import LambdaLR
class Objective(Module, ABC):
def __init__(self, loc, optimum):
super().__init__()
self.loc = Parameter(torch.Tensor(loc))
self.optimum = torch.Tensor(optimum)
@abstractmethod
def loss(self, loc):
raise NotImplementedError
def forward(self):
return self.loss(self.loc)
A simple quadratic objective (easy to solve)
class Quadratic(Objective):
def __init__(self, loc, sigma=((1, 0), (0, 1)), optimum=(0, 0), div=1.):
super().__init__(loc=loc, optimum=optimum)
self.prec = torch.inverse(torch.Tensor(sigma))
self.div = div
def loss(self, loc):
diff = loc - self.optimum
return torch.einsum('...a,ab,...b->...', diff, self.prec, diff) / self.div
The Rosenbrock objective (hard to solve)
class RosenbrockFunction(Objective):
def __init__(self, a=1.0, b=100.0, loc=(0, 0)):
super().__init__(loc=loc, optimum=[a, a ** 2])
self.a = a
self.b = b
def loss(self, loc):
# Rosenbrock function calculation
return (self.a - loc[..., 0]) ** 2 + self.b * (loc[..., 1] - loc[..., 0] ** 2) ** 2
A function for running the optimisation and plotting the results
import matplotlib.pyplot as plt
def optimise(module_kwargs,
module_class=Quadratic,
plot_range=((-10, 10), (-10, 10)),
n_grid=50,
n_iterations=100,
lr=1.,
warm_up=1
):
# optimise and collect trace
module = module_class(**module_kwargs)
optimizer = Adam(module.parameters(), lr=lr)
scheduler = LambdaLR(optimizer, lr_lambda=lambda step: step / warm_up if step < warm_up else 1)
trace = [module.loc.clone().detach()]
for it in range(n_iterations):
optimizer.zero_grad()
loss = module()
loss.backward()
optimizer.step()
scheduler.step()
trace += [module.loc.clone().detach()]
# plot
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
# plot objective landscape
x_grid = torch.linspace(*plot_range[0], n_grid)
y_grid = torch.linspace(*plot_range[1], n_grid)
xy = torch.meshgrid([x_grid, y_grid])
# flatten and concatenate along new dimension to get grid of coordinates
locs = torch.cat(tuple(l.flatten()[..., None] for l in xy), dim=-1)
# evaluate function on grid
f = module.loss(locs).reshape(n_grid, n_grid).transpose(-2, -1)
ax.contourf(x_grid, y_grid, f, 100, zorder=-10, cmap='Reds_r')
# optimum
ax.scatter(*module.optimum, marker='+', c='g', zorder=100, label='optimum')
# trace
c = (0.1, 0.1, 0.1)
trace = torch.cat(tuple(t[None, :] for t in trace)).clone().detach().numpy()
ax.plot(*trace.transpose(), '-o', linewidth=1, markersize=3, color=c, label='trace')
ax.scatter(*trace[0], s=5, color=c, zorder=0)
# adjust stuff
ax.legend()
ax.set_aspect('equal')
ax.set_xlim(*plot_range[0])
ax.set_ylim(*plot_range[1])
fig.tight_layout()
plt.show()
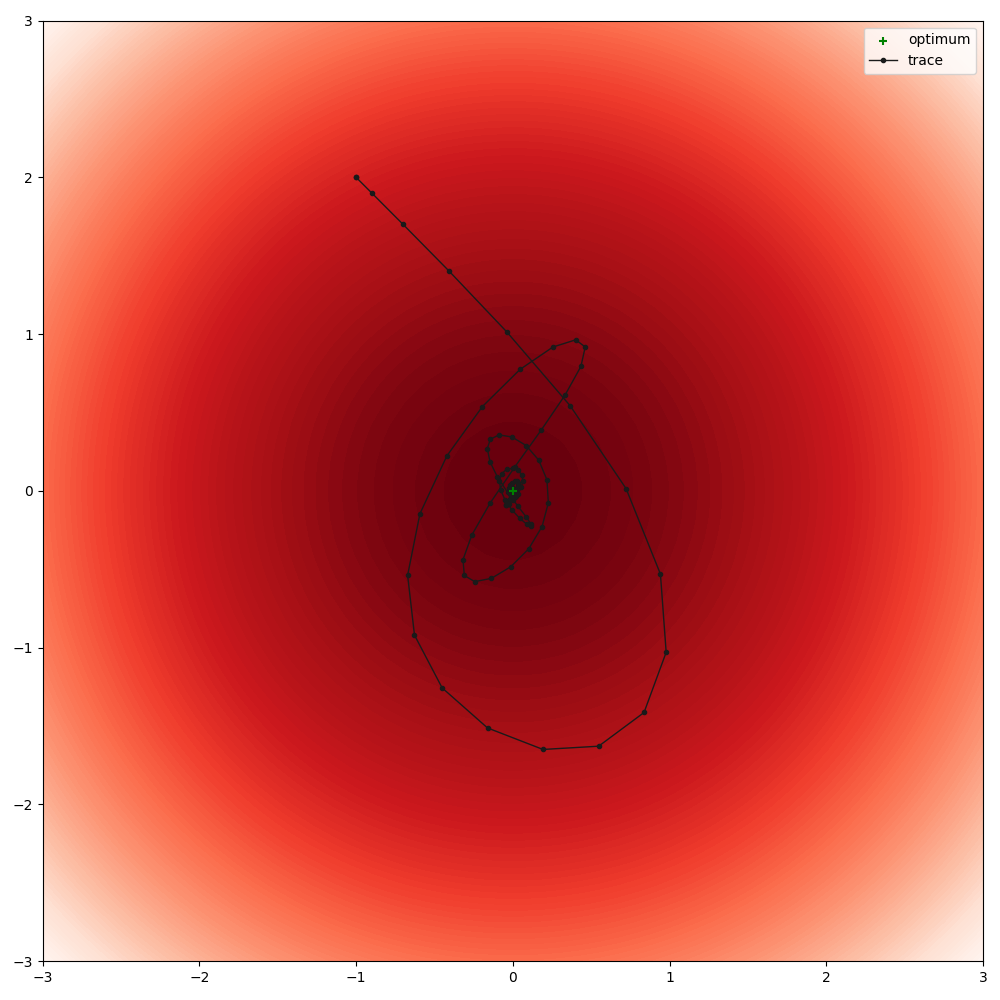
Run optimisation for simple quadratic objective (slightly too high learning rate to provoke overshooting)
optimise(
module_class=Quadratic,
module_kwargs=dict(loc=[-1, 2], sigma=[[1, 0], [0, 1]]),
plot_range=((-3, 3), (-3, 3)),
lr=1,
warm_up=10,
)
/home/runner/.local/lib/python3.12/site-packages/torch/functional.py:554: UserWarning:
torch.meshgrid: in an upcoming release, it will be required to pass the indexing argument. (Triggered internally at /pytorch/aten/src/ATen/native/TensorShape.cpp:4322.)
For axis-aligned anisotropies, Adam’s adaptive learning rate works well
optimise(
module_class=Quadratic,
module_kwargs=dict(loc=[-2, 1], sigma=[[100, 0], [0, 1]]),
plot_range=((-3, 3), (-3, 3)),
lr=0.1,
n_iterations=100,
warm_up=10,
)
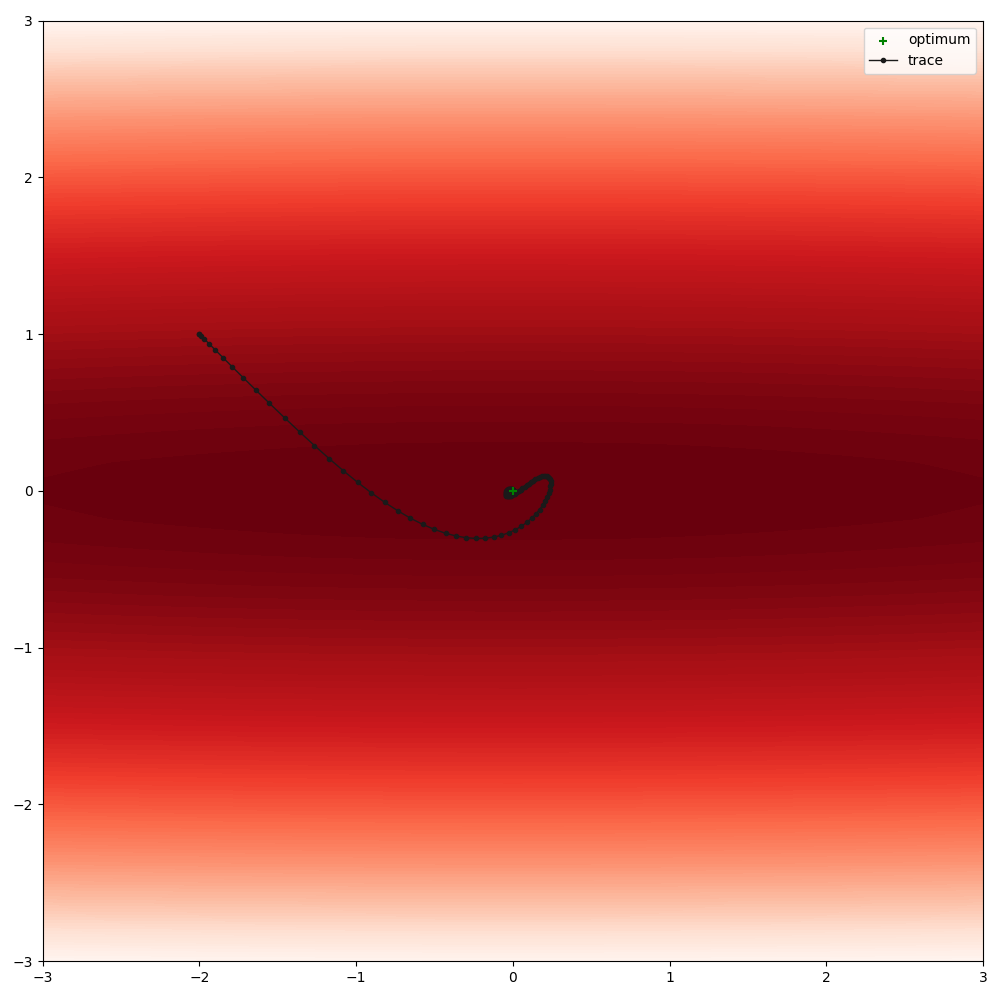
For non-aligned anisotropies, Adam’s adaptive learning rate fails (same settings)
optimise(
module_class=Quadratic,
module_kwargs=dict(loc=[-2, 1], sigma=[[1, -0.99], [-0.99, 1]]),
plot_range=((-3, 3), (-3, 3)),
lr=0.1,
n_iterations=100,
warm_up=10,
)
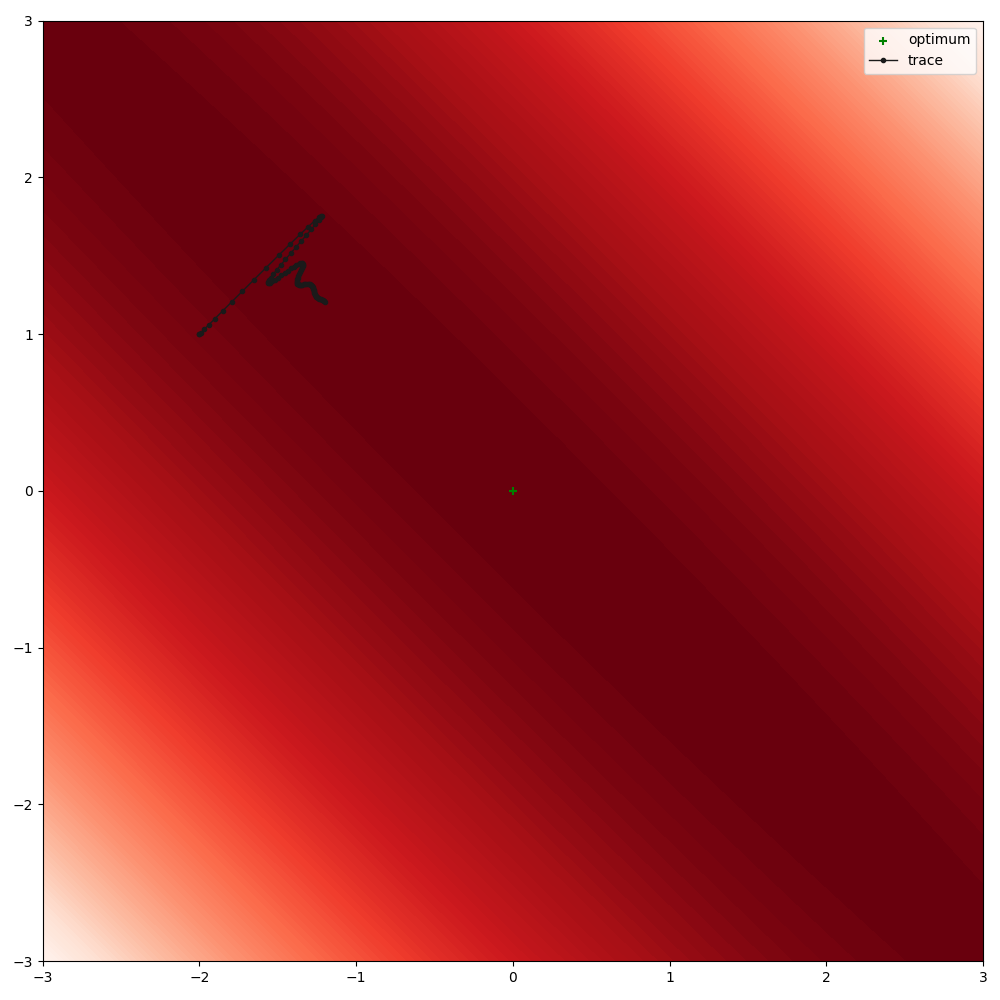
A non-trivial case where this becomes relevant is the Rosenbrock objective
optimise(
module_class=RosenbrockFunction,
module_kwargs=dict(a=1.5, b=100, loc=[-1.2, 1]),
plot_range=((-3, 3), (-3, 3)),
lr=1,
warm_up=10,
)
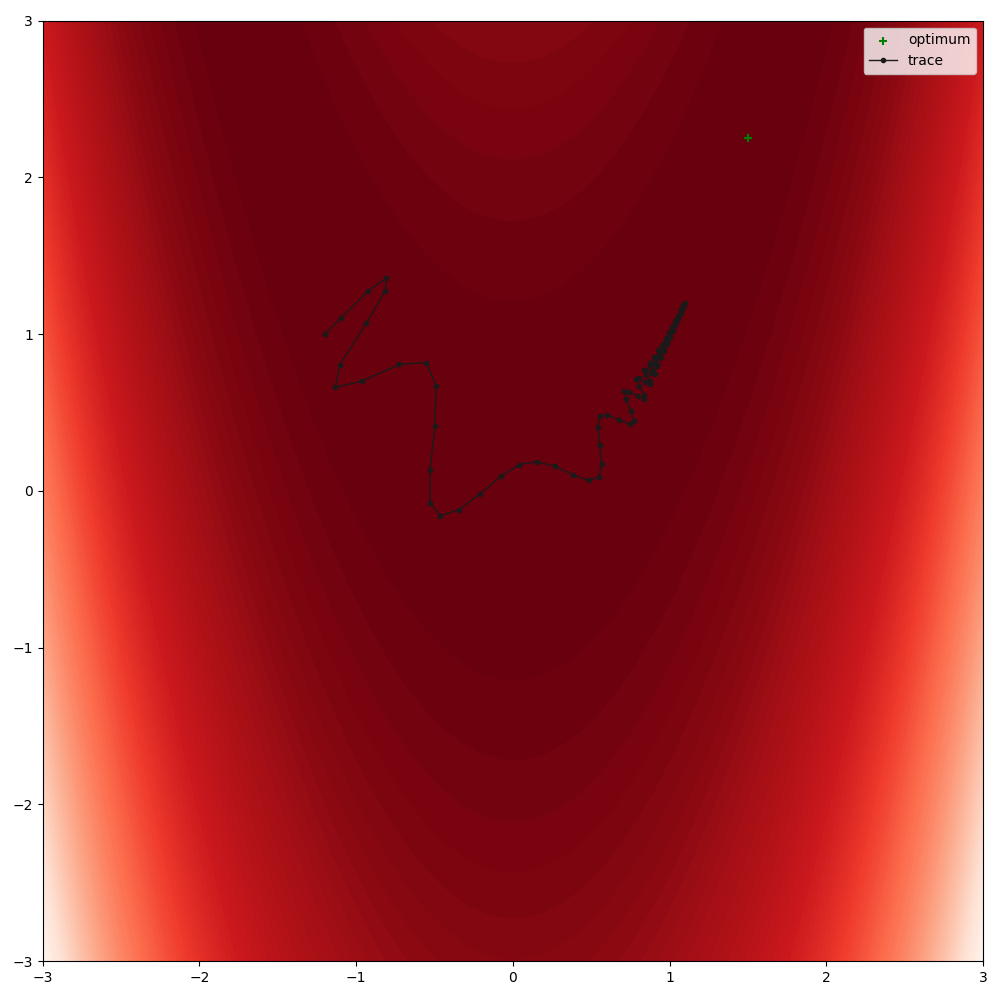
Total running time of the script: (0 minutes 0.687 seconds)